1. 삽입 정렬(Insertion Sort)
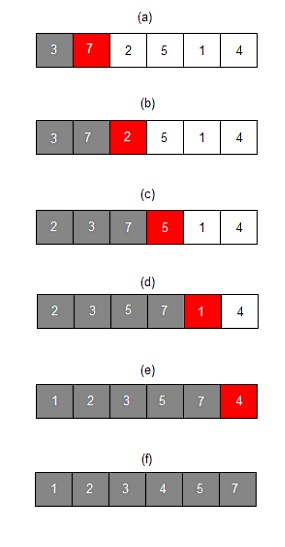
가장 단순한 정렬 알고리즘 중의 하나로써 이미 정렬되어 있는 서브 파일에 새로운 한 개의 레코드를 입력하여 그 순서를 삽입시킨다. 쉽게는 자신보다 앞의 레코드 값이 큰지 작은지 비교를 해서 자신의 위치를 찾아 삽입하는 정렬이다. 따라서 앞의 레코드 값과 비교해야 하기 때문에 배열 인덱스 0 부터 시작으로 생각하면 1부터 비교를 시작한다. ( arr[1] ~ arr[n-1] )
삽입을 하면 배열이 계속 밀리기 때문에 배열의 사이즈가 크면 클수록 비효율적. 시간복잡도는 O(n^2)
삽입 정렬은 안정 정렬이다. 안정 정렬이란 동일한 값에 대해 기존의 순서가 유지되는 정렬 방식 ( 버블 정렬, 삽입 정렬 )
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 |
public class Sort { public static void main(String[] args) { int arr[]= {7,3,5,2,1,8,9,4}; arr = insertion_sort(arr); for(int i=0; i<arr.length; i++) { System.out.print(arr[i]+" "); } }
public static int[] insertion_sort(int arr[]) { for(int i=1; i<arr.length; i++) { int tmp = arr[i]; int j=i; while(j>0 && arr[j-1] > tmp) { arr[j] = arr[j-1]; j--; } arr[j] = tmp; } return arr; } }
|
cs |
2. 버블 정렬(Bubble Sort)
버블 정렬의 기본 전략은 주어진 파일에서 인접한 레코드의 두 개의 키를 비교하여 그 크기에 따라 레코드의 위치를 서로 교환해 준다. 즉 첫 번째와 두 번쨰 키를 비교하여 첫 번째가 두 번째보다 크다면 위치를 교환하고 그 다음에 두 번쨰에 위치한 레코드의 키와 세 번째 키를 비교하여 전술한 과정을 수행한다. 이 과정을 맨 마지막 레코드까지 수행했을 때 가장 큰 값의 키를 갖는 레코드가 맨 마지막에 위치하게 된다. 2회전에서는 마지막 레코드는 제외하고 비교, 교환의 작업을 수행하게 된다.
이렇게 정렬을 1회전 수행할 때마다 정렬에서 제외되는 데이터가 하나씩 늘어난다. 레코드의 수를 n이라 할 때 최대(n-1) 회전을 수행해야 하지만 어느 회전에서든 레코드의 위치 교환이 발생하지 않으면 주어진 파일은 완전히 오름차순으로 순서 배열이 된 셈이다.
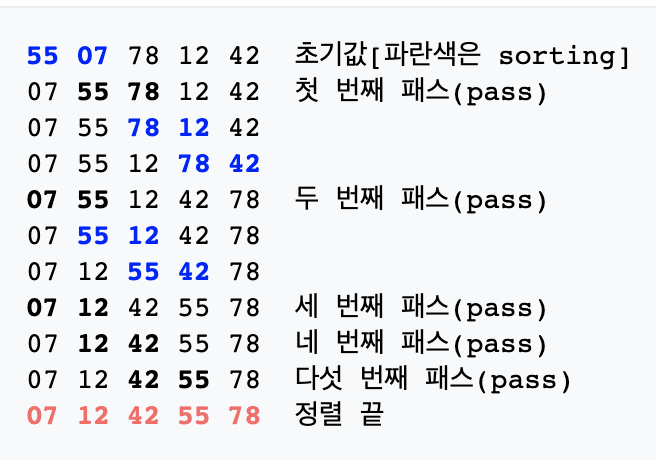
레코드의 값을 바꾸어 줄때 마다 swap하는 시간이 비효율적. 시간 복잡도는 O(n^2)
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 |
public class Sort { public static void main(String[] args) { int arr[]= {7,3,5,2,1,8,9,4}; // arr = insertion_sort(arr); arr = bubble_sort(arr); for(int i=0; i<arr.length; i++) { System.out.print(arr[i]+" "); } } public static int[] bubble_sort(int arr[]) { for(int i=arr.length-1; i>0; i--) { for(int j=0; j<i; j++) { if(arr[j] > arr[j+1]) { int tmp = arr[j]; arr[j] = arr[j+1]; arr[j+1] = tmp; } } } return arr; } } |
cs |
3. 선택 정렬(Selection Sort)
선택 정렬은 버블 정렬과 함께 가장 많이 사용되는 정렬 방법 중의 하나이다. 선택 정렬은 버블 정렬이 순서를 바꾸는 Swap 작업을 보완하는 방식이다.
오름차순의 경우, 첫 번째 요소와 두 번째 요소를 비교하여 순서 조정, 첫 번째 요소와 세 번째 요소의 순서 조정, .... , 첫 번째 요소와 N 번째 요소의 순서 조정을 거치면서 n개의 레코드로부터 최소값을 첫 번째 위치로 놓는 것이 1단계의 결과이고, 최종적으로 (N-1)번째 레코드와 N 번째 레코드 중에서 키 값이 작은 레코드를 (N-1) 번째에 놓음으로써 수행은 완료된다.
시간 복잡도는 O(N^2)이다.
선택 정렬은 불안정 정렬이다. 불안정 정렬이란 동일한 값에 대해 기존의 순서가 유지되지 않는 정렬 방식 ( 선택 정렬 )

|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 |
public class Sort { public static void main(String[] args) { int arr[]= {7,3,5,2,1,8,9,4}; // arr = insertion_sort(arr); // arr = bubble_sort(arr);
arr = selection_sort(arr); for(int i=0; i<arr.length; i++) { System.out.print(arr[i]+" "); } }
public static int[] selection_sort(int arr[]) { for(int i=0; i<arr.length-1; i++) { int min_index = i; for(int j=i+1; j<arr.length; j++) { if(arr[j] < arr[min_index]) min_index = j; } int tmp = arr[min_index]; arr[min_index] = arr[i]; arr[i] = tmp; }
return arr; } }
|
cs |
4. 퀵 정렬(Quick Sort)
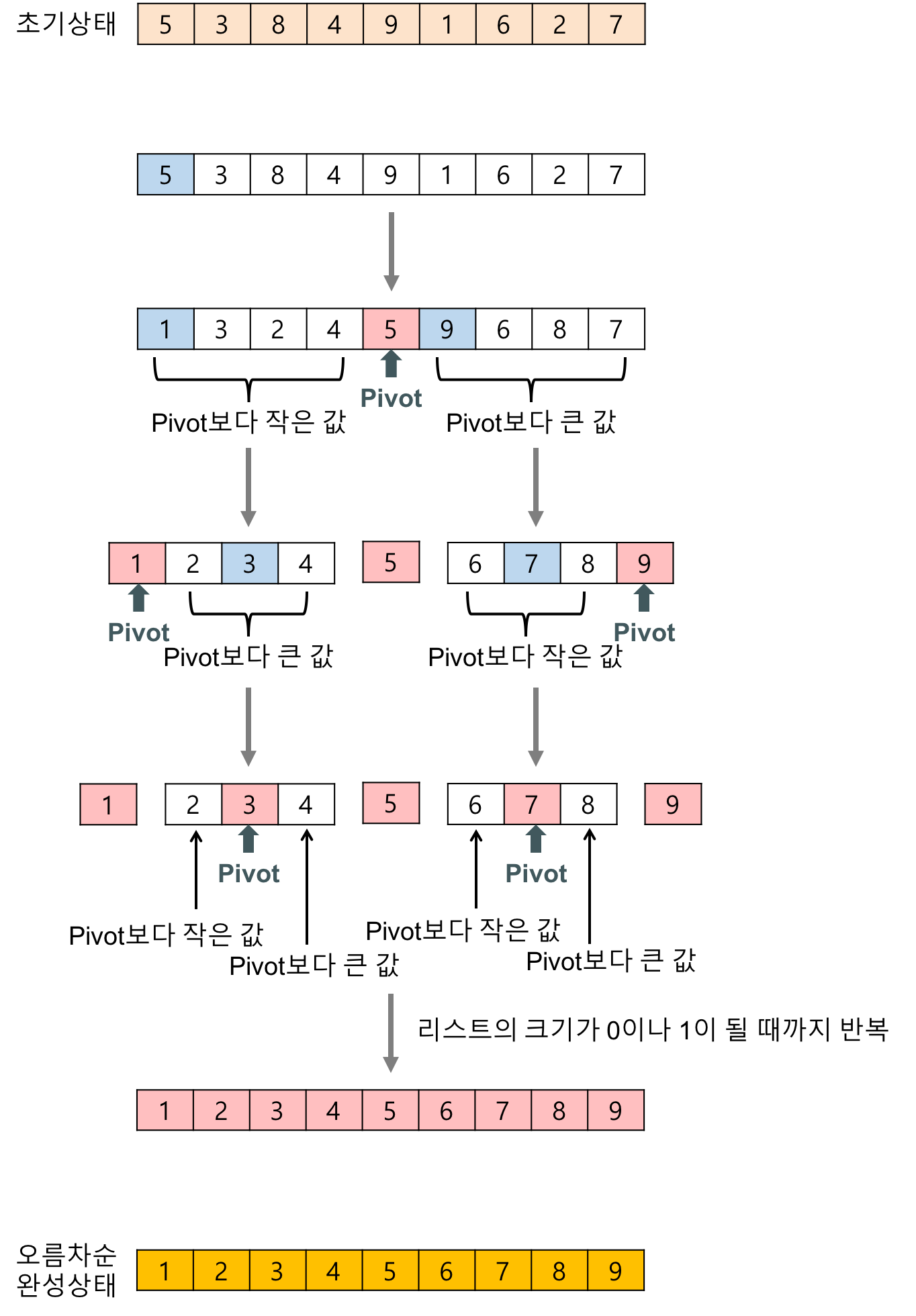
퀵 정렬 알고리즘은 다른 알고리즘에 비해 평균 수행 능력이 양호하다고 평가된다. 이것은 분할 정복 방식이고, 순환 알고리즘으로써 주어진 ㅊ파일에다 퀵 정렬 알고리즘을 적용하면 특정한 키(Pivot) 값보다 작은 값을 갖는 레코드와 큰 값을 레코드로 분리되어 한 개의 파일이 논리적으로 두 개의 서브파일로 재배열된다. 각각의 서브 파일에다 퀵 정렬 알고리즘을 적용하는 과정을 반복하면 최종으로 완전히 순서 배열된 파일이 얻어진다.
간단히 말하면 특정한 레코드값(Pivot)을 중심으로 그 왼쪽에는 피봇값보다 작은 레코드가 배열되고, 오른쪽에는 큰 레코드가 놓이게 된다.
평균적인 시간 복잡도는 O(NlogN)이다. 속도가 빠르고 추가적인 공간을 필요로 하지 않는다.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 |
public class Sort { static int arr[]= {7,3,5,2,1,8,9,4}; public static void main(String[] args) {
// arr = insertion_sort(arr); // arr = bubble_sort(arr); // arr = selection_sort(arr); quick_sort(arr, 0, arr.length-1); for(int i=0; i<arr.length; i++) { System.out.print(arr[i]+" "); } } public static void quick_sort(int arr[], int begin, int end) { if(begin>=end) return;
int pivot = begin; int i=begin+1; int j=end;
while(i<=j) { while(i<=end && arr[i]<=arr[pivot]) i++; while(j>begin && arr[j]>=arr[pivot]) j--;
if(i<=j) { int tmp = arr[i]; arr[i] = arr[pivot]; arr[pivot] = tmp; }else { int tmp = arr[j]; arr[j] = arr[pivot]; arr[pivot] = tmp; }
}
quick_sort(arr,begin, j-1); quick_sort(arr, j+1, end); } public static int[] selection_sort(int arr[]) { for(int i=0; i<arr.length-1; i++) { int min_index = i; for(int j=i+1; j<arr.length; j++) { if(arr[j] < arr[min_index]) min_index = j; } int tmp = arr[min_index]; arr[min_index] = arr[i]; arr[i] = tmp; }
return arr; } } |
cs |
5. 힙 정렬(Heap Sort)
힙 정렬은 힙이라는 데이터 구조를 이용한 알고리즘이다. 힙 구조는 전 이진 트리로써 각 노드의 키 값이 자식 노드의 키 값보다 작지 않은 특징을 가지고 있다. 전 이진 트리로 힙을 구성할 때는 가장 낮은 레벨의 우측 노드부터 그의 부모 노드와 비교하여 자식 노드가 크면 부모 노드와 교환하는 작업을 수행한다.
힙은 최대 힙과 최소 힙이 있는데, 최대 힙은 자식 노드보다 부모 노드의 값이 크게 구성된 경우를 말하고 최소 힙은 반대로 자식 노드보다 부모 노드의 값이 작게 구성된 경우이다.
힙이 일단 구성된 다음, 가장 큰 값을 찾아내고 나머지 노드를 사용하여 힙을 재구성한다. 여기에서 또 두 번째로 큰 값을 찾아낸다. 이러한 작업을 반복하여 트리의 크기를 줄여가면서 수행한다. 시간복잡도는 최악, 최선, 평균 모두 O(nlogn) 이다.
힙 정렬의 특징
- 정렬을 수행하기 위해 n만큼의 기억 공간이 필요하다.
- 정렬을 수행하는 속도가 빠르다.
- 부모 노드의 위치는 index/2이다.
- 각 노드의 좌측 자식 노드는 2*index이고, 우측 자식의 노드는 2*index+1이다.

|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 |
public class Sort { static int arr[]= {7,3,5,2,1,8,9,4}; public static void main(String[] args) {
// arr = insertion_sort(arr); // arr = bubble_sort(arr); // arr = selection_sort(arr); // quick_sort(arr, 0, arr.length-1); heapSort(arr); for(int i=0; i<arr.length; i++) { System.out.print(arr[i]+" "); } }
public static void heapify(int array[], int n, int i) { int p = i; int l = i * 2 + 1; int r = i * 2 + 2;
if (l < n && array[p] < array[l]) { p = l; }
if (r < n && array[p] < array[r]) { p = r; }
if (i != p) { swap(array, p, i); heapify(array, n, p); } }
public static void heapSort(int[] array) { int n = array.length;
// init, max heap for (int i = n / 2 - 1; i >= 0; i--) { System.out.println(i); heapify(array, n, i); }
// for extract max element from heap for (int i = n - 1; i > 0; i--) { swap(array, 0, i); heapify(array, i, 0); } }
public static void swap(int[] array, int a, int b) { int temp = array[a]; array[a] = array[b]; array[b] = temp; } }
|
cs |
6. 병합 정렬(Merge Sort)
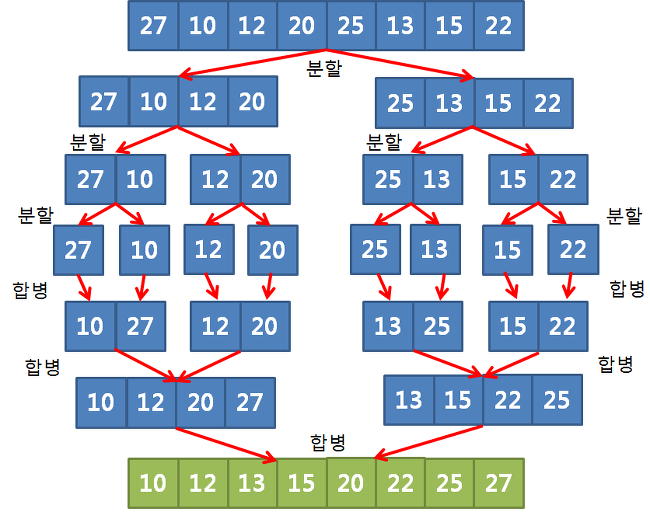
‘존 폰 노이만(John von Neumann)’이라는 사람이 제안한 방법으로써 분할 정복 알고리즘이며 O(n log n)의 시간 복잡도를 갖는 비교 기반 정렬 알고리즘이다. 간단하게 말하면 하나의 배열을 두 개의 균등한 크기로 분할하고 분할된 부분 배열을 정렬한 다음, 두 개의 정렬된 부분 배열을 합쳐 전체가 정렬된 배열이 되게 하는 방법이다.
분할 정복(divide and conquer) 방법이란
문제를 작은 문제로 분리하고 각각을 해결한 다음, 결과를 모아서 원래의 문제를 해결하는 방식이다.
분할 정복 방법은 보통 재귀 방식을 이용하여 구현한다.
단점으로는 임시 배열이 필요하다는 점이다. 시간 복잡도는 O(n log n)이다.
합병 정렬은 다음과 같이 작동한다.
- 리스트의 길이가 1 이하이면 이미 정렬된 것으로 본다. 그렇지 않은 경우에는
- 분할(divide) : 정렬되지 않은 리스트를 절반으로 잘라 비슷한 크기의 두 부분 리스트로 나눈다.
- 정복(conquer) : 각 부분 리스트를 재귀적으로 합병 정렬을 이용해 정렬한다.
- 결합(combine) : 두 부분 리스트를 다시 하나의 정렬된 리스트로 합병한다. 이때 정렬 결과가 임시배열에 저장된다.
- 복사(copy) : 임시 배열에 저장된 결과를 원래 배열에 복사한다.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 |
public class Sort { static int arr[]= {7,3,5,2,1,8,9,4}; public static void main(String[] args) {
// arr = insertion_sort(arr); // arr = bubble_sort(arr); // arr = selection_sort(arr); // quick_sort(arr, 0, arr.length-1); // heapSort(arr); mergeSort(arr, 0, arr.length-1); for(int i=0; i<arr.length; i++) { System.out.print(arr[i]+" "); } }
private static void mergeSort(int[] arr, int m, int n) { // TODO Auto-generated method stub if(m<n) { int middle=(m+n)/2; mergeSort(arr,m,middle); mergeSort(arr,middle+1,n); merge(arr,m,middle,n); }
}
private static void merge(int[] arr, int m, int middle, int n) { // TODO Auto-generated method stub int i=m; int j=middle+1; int t=1; int tmp[]=new int[arr.length+1];
while(i<=middle && j<=n) { if(arr[i]<arr[j]) { tmp[t++]=arr[i++]; }else { tmp[t++]=arr[j++]; } }
while(i<=middle) { tmp[t++]=arr[i++]; } while(j<=n) { tmp[t++]=arr[j++]; }
i=m; t=1;
while(i<=n) { arr[i++]=tmp[t++]; } } } |
cs |
'알고리즘' 카테고리의 다른 글
| #알고리즘_선형 탐색/이진 탐색 - Java (0) | 2020.01.08 |
|---|---|
| #알고리즘_신장 트리(Spanning Tree) (0) | 2020.01.08 |
| #알고리즘_프림(Prim Algorithm) - Java (0) | 2020.01.08 |
| #알고리즘_크루스칼(Kruskal Algorithm) - Java (0) | 2020.01.07 |
| #알고리즘_다익스트라(Dijkstra Algorithm) - Java (0) | 2020.01.07 |