#유형 : 수학
#난이도 : lv2

|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
|
class Solution {
public long solution(long w, long h) {
long answer = 1;
long tmp = Math.max(w,h);
long tmp2 = Math.min(w,h);
w = tmp2;
h = tmp;
answer = w * h - (w+h-gcd(h,w));
return answer;
}
public long gcd(long x, long y){
if(x % y == 0)
return y;
return gcd(y, x%y);
}
}
|
cs |
이런 문제의 경우, 보통 여러 케이스를 그려가며 반복되는 공통점을 찾는다.
우선 짝수의 경우를 먼저 살펴보자
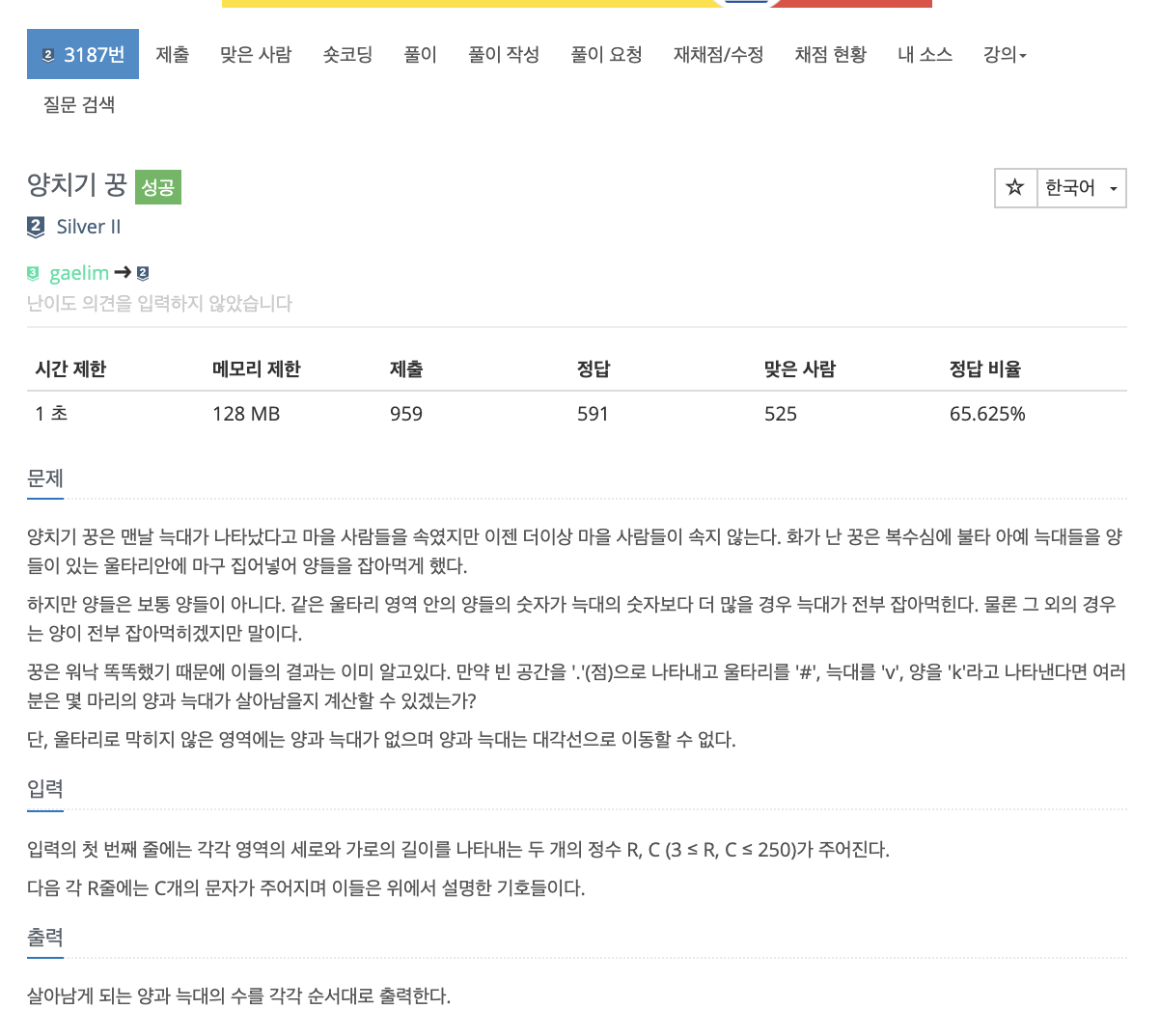
8 x 12의 경우 96 - 16개
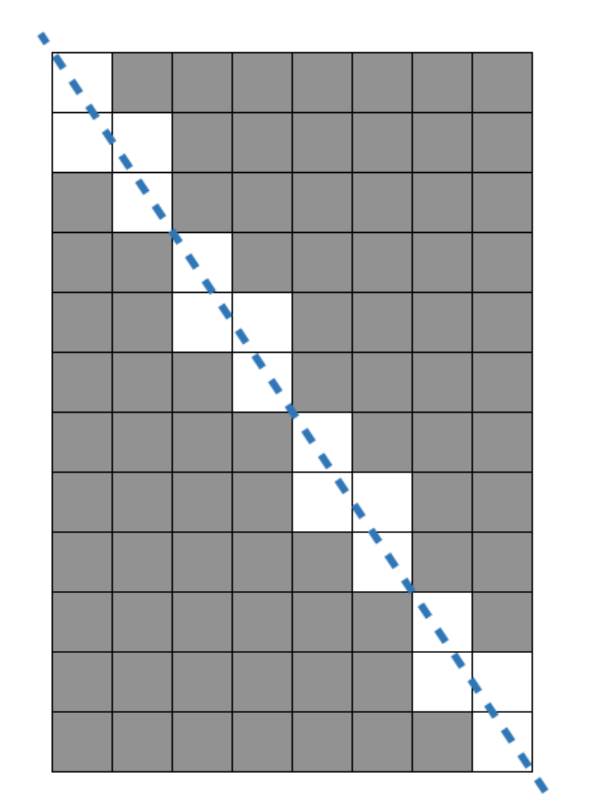
6 x 9의 경우 54 - 12개

4 x 6 의 경우 24 - 8
이 때, 사용할 수 없는 직사각형의 공통점은 w+h-(w,h)의 최대공약수 라는 것을 확인할 수 있다.
그렇다면 홀수의 경우에도 같은 방법이 적용되는지 확인해보자.

3 x 4 의 경우 12 - 6
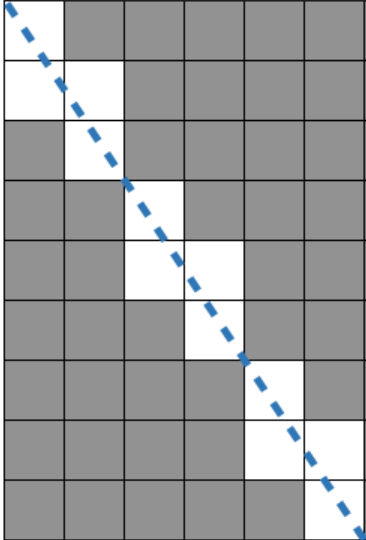
2 x 3 의 경우 6 - 4
둘다 홀수인 경우에도 W + H - ((W,H)의 최대공약수 1) 이 적용되는 것을 확인할 수 있다.
마지막으로, 홀수와 짝수가 같이 있는 경우를 살펴보자

1 x 2 의 경우 2 - 2
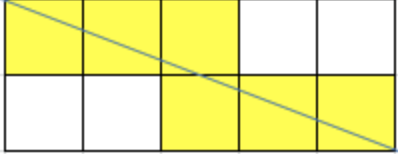
5 x 2 의 경우 10 - 6
아까와 동일하다.
결과로, 사용할 수 없는 직사각형의 공통점은 w+h-(w,h)의 최대공약수가 맞다는 것을 확인할 수 있다.
'프로그래머스' 카테고리의 다른 글
| #프로그래머스_튜플 - Java 자바 (0) | 2021.12.10 |
|---|---|
| #프로그래머스_오픈채팅방 - Java 자바 (0) | 2021.12.08 |
| #프로그래머스_섬 연결하기 - Java 자바 (0) | 2020.06.28 |
| #프로그래머스_가장 먼 노드 - Java 자바 (0) | 2020.06.25 |
| #프로그래머스_예산 - Java 자바 (0) | 2020.06.25 |